Regresión lineal, outliers y personas en datos reales
La semana pasada un amigo me comentó que iba a vender su departamento.
Le pregunté cuánto esperaba obtener de la venta, y me dio un número abismalmente alto.
No era “un poco por encima del mercado”.
Era un valor que, de verlo en un dataset, lo hubiera marcado inmediatamente como outlier.
Mi reacción fue automática: ese precio no tiene sentido.
La segunda fue más incómoda: ¿cómo explicaría esto un modelo?
La tercera, inevitable: ¿debería eliminarlo antes de entrenar?
Este artículo nace ahí.
No como un ejercicio académico, sino como una reflexión técnica sobre qué hace realmente una regresión lineal cuando se enfrenta a datos reales, outliers reales y decisiones humanas reales.
Un dataset real: de California a Caballito
En muchos cursos introductorios —y en buena parte de la documentación— la regresión lineal suele explicarse sobre datasets clásicos, como California Housing. Son datasets excelentes para enseñar: limpios, consistentes, bien documentados y pensados para que el algoritmo se luzca.
El problema es que casi ningún dato real se parece a California Housing.
El dataset que uso acá no salió de una librería ni de un repositorio académico. Proviene de un proyecto personal de ingeniería de datos que recolecta avisos inmobiliarios publicados en la Ciudad de Buenos Aires. Es un ETL diseñado para capturar lo que efectivamente aparece en portales inmobiliarios, no para optimizar métricas ni facilitar ejemplos.
Para este análisis tomé un subconjunto deliberadamente pequeño y acotado, casi como un contrapunto explícito a los datasets académicos:
- barrio: Caballito
- radio geográfico: 0.9 km desde el centro del barrio
(lat: -34.6180, long: -58.4410) - fecha de extracción: 24 de diciembre de 2025
- tamaño de muestra: n = 23 avisos
Cada observación incluye, como mínimo:
- superficie total (m²),
- precio de publicación (USD).
A diferencia de California Housing, este dataset:
- tiene valores faltantes,
- presenta unidades no siempre normalizadas,
- contiene descripciones heterogéneas,
- y puede incluir errores de carga.
Nada de eso es accidental. Es exactamente lo que aparece cuando uno trabaja con datos reales.
El tamaño reducido de la muestra tampoco es una limitación involuntaria. Es una decisión metodológica.
No estoy intentando construir un modelo predictivo ni competir con datasets curados. Estoy intentando ver qué resuelve matemáticamente una regresión lineal cuando se la saca del entorno protegido de los ejemplos académicos y se la enfrenta a datos que no fueron diseñados para lucirse.
Pasar de California Housing a Caballito no es solo un cambio de geografía. Es un cambio de expectativas.
El modelo más simple posible (y por qué)
Hace algunos meses completé Matrix Algebra for Engineers en Coursera. En uno de sus módulos, Jeffrey R. Chasnov desarrolla el problema de la minimización de cuadrados utilizando matrices, mostrando cómo puede derivarse analíticamente la recta que mejor ajusta un conjunto de datos. Lo que sigue a continuación es un ejemplo real de esa matemática subyacente.
Trabajo con una única variable independiente: superficie.
El modelo es el clásico:
\[y = \beta_0 + \beta_1 x\]En forma matricial:
\[A\vec{\beta} = \vec{y}\]donde:
\[A = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{bmatrix}, \qquad \vec{\beta} = \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix}, \qquad \vec{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}\]Este sistema es sobredeterminado.
Con datos reales, el sistema casi nunca es consistente: $\vec{y}$ no cae exactamente en el espacio columna de $A$.
No hay solución exacta.
Y eso no es un defecto del modelo: es la situación normal cuando hay ruido, heterogeneidad y decisiones humanas detrás de los números.
Qué problema matemático resuelve realmente la regresión lineal
La regresión lineal no resuelve $A\vec{\beta} = \vec{y}$.
Resuelve este problema:
\[\min_{\vec{\beta}} \; \|\vec{y} - A\vec{\beta}\|^2\]Es decir, busca los coeficientes que minimizan:
\[\sum_{i=1}^{n} (y_i - (\beta_0 + \beta_1 x_i))^2\]Este detalle —el cuadrado— es clave para todo lo que sigue.
Al elevar el error al cuadrado:
- evitamos cancelación de signos,
- penalizamos errores grandes más que errores pequeños,
- y hacemos que ciertos puntos tengan una influencia desproporcionada.
Derivando esta expresión en forma matricial se llega a las ecuaciones normales:
\[A^\top A \vec{\beta} = A^\top \vec{y}\]Si $A^\top A$ es invertible:
\[\hat{\vec{\beta}} = (A^\top A)^{-1} A^\top \vec{y}\]No hay heurística.
No hay intuición.
Hay álgebra matricial pura.
Porque cuando una regresión devuelve una pendiente poco intuitiva o un intercepto difícil de justificar, el impulso es culpar al algoritmo (¡o peor aún! tocar el random_state creyendo que ese gesto cosmético puede mejorar mágicamente la capacidad predictiva). Haber visto la derivación completa nos obliga a aceptar algo incómodo:
el modelo no toma decisiones; obedece exactamente a la estructura de los datos.
Si todo esto suena abstracto, el punto clave es este: la regresión no ‘decide’ qué es razonable; nosotros lo hacemos al definir qué datos entran.
Un ejemplo concreto: números que no opinan
Tomemos tres observaciones reales de mi propio dataset (solo para ilustrar el cálculo):
| Superficie (m²) | Precio (USD) |
|---|---|
| 31 | 72.000 |
| 43 | 124.000 |
| 76 | 142.000 |
Las matrices son:
\[A = \begin{bmatrix} 1 & 31 \\ 1 & 43 \\ 1 & 76 \end{bmatrix}, \qquad \vec{y} = \begin{bmatrix} 72000 \\ 124000 \\ 142000 \end{bmatrix}\]Y las ecuaciones normales:
\[A^\top A = \begin{bmatrix} 3 & 150 \\ 150 & 8278 \end{bmatrix}, \qquad A^\top \vec{y} = \begin{bmatrix} 338000 \\ 18884000 \end{bmatrix}\]La solución depende de todas las observaciones.
Cambiar una sola fila de $A$ cambia $A^\top A$ y cambia la recta.
Con $n$ chico, esto se nota mucho.
Con $n$ grande, se diluye.
Pero el mecanismo es exactamente el mismo.
Resultados del ajuste y visualización
Al aplicar una regresión lineal simple sobre el dataset completo (superficie vs. precio), el ajuste arroja:
- R² = 0.641
- n = 23 observaciones
Para un dataset real, pequeño y no curado, este valor no es despreciable.
Pero tampoco habilita a hablar de capacidad predictiva.
Con $n=23$, este valor debe leerse con cautela: pequeñas variaciones en la muestra o la inclusión/exclusión de un solo punto pueden alterar significativamente el ajuste.
La pendiente representa un incremento promedio del precio por metro cuadrado, pero no debe interpretarse como una ley de mercado.
La ordenada al origen carece de interpretación económica directa: es un artefacto matemático necesario para resolver el sistema, no una afirmación sobre el valor de un departamento de 0 m².
Dos visualizaciones ayudan más que cualquier métrica:
- el scatter plot superficie–precio con la recta ajustada,
- el gráfico de residuos, donde se observa claramente que el error no es ruido blanco.
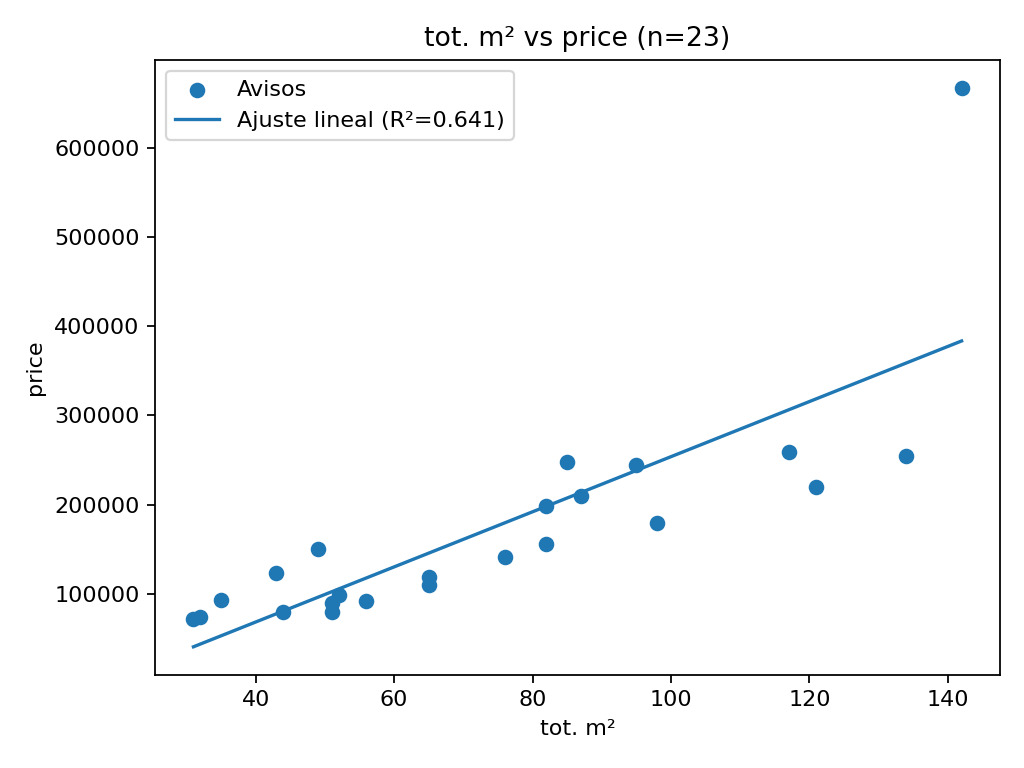
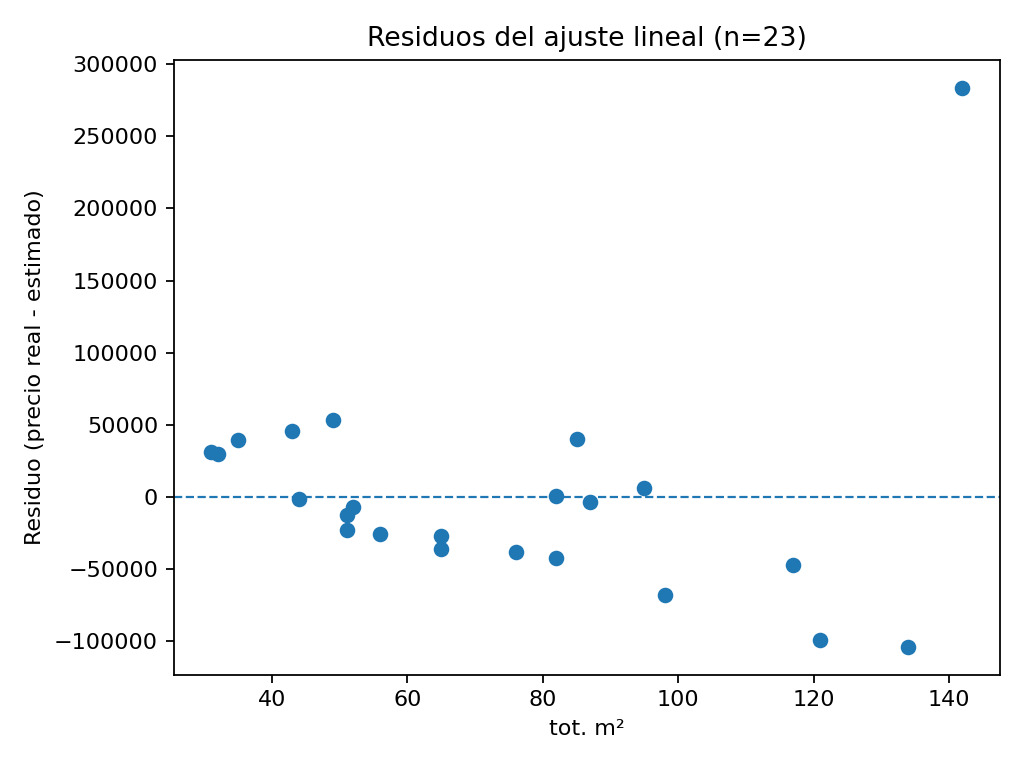
El gráfico de residuos sugiere estructura: en este subconjunto chico, el modelo tiende a subestimar en superficies bajas y a sobreestimar en superficies altas, además de un punto extremo que concentra gran parte del error.
Volviendo al departamento “demasiado caro”
El precio que me dijo mi amigo no era un error de carga.
No era un typo.
Era una decisión consciente.
Desde el punto de vista matemático, ese punto:
- tiene un residuo grande,
- y al elevarse al cuadrado, pesa mucho en la función objetivo.
Desde el punto de vista humano, ese precio tiene historia:
- expectativas,
- apego,
- recuerdos,
- urgencias o ausencia de ellas.
La regresión no distingue nada de eso.
Solo ve números.
Outliers: el gesto automático y el gesto reflexivo
En ingeniería de datos hay un gesto muy común:
“Eliminar outliers”.
Muchas veces se hace de forma automática:
- se aplica un IQR,
- se cortan percentiles,
- se descarta lo que “rompe el modelo”.
Matemáticamente, eliminar outliers suele:
- estabilizar coeficientes,
- mejorar métricas,
- producir rectas más prolijas.
Pero esa prolijidad tiene un costo conceptual.
Esa automatización suele mezclar casos distintos: a veces son errores de carga y conviene corregirlos; otras veces son casos reales que el modelo no sabe explicar.
Qué significa eliminar un outlier, en términos matemáticos
Eliminar un outlier no es una operación neutral.
Implica:
- quitar una fila de $A$,
- quitar una componente de $\vec{y}$,
- cambiar $A^\top A$,
- cambiar su inversa,
- y cambiar la solución completa del sistema.
No estamos “limpiando ruido blanco”.
Estamos redefiniendo el problema que el modelo resuelve.
A veces eso es correcto.
Otras veces, no.
Qué significa eliminar un outlier, en términos humanos
Este es el punto que suele omitirse.
Detrás de un outlier hay una persona:
- alguien que sobrevalúa su propiedad,
- alguien que necesita vender rápido,
- alguien que heredó,
- alguien que se está separando,
- alguien que no quiere vender realmente.
Eliminar ese punto es decir:
“esta historia no entra en el modelo”.
A veces es una decisión razonable.
Otras veces es una pérdida de información.
El experimento con random_state como síntoma
En una prueba aparte, repetí un train/test split cambiando solo el random_state, y los coeficientes variaban.
No es magia.
Cambiar el split cambia el conjunto de filas que entran en $A$ y en $\vec{y}$:
\[\hat{\vec{\beta}}_{\text{train}} = (A_{\text{train}}^\top A_{\text{train}})^{-1} A_{\text{train}}^\top \vec{y}_{\text{train}}\]Si un outlier entra o sale del entrenamiento, la solución cambia.
Ese comportamiento no indica que el modelo sea malo.
Indica que el dataset es sensible.
Y esa sensibilidad es información valiosa.
¿Puede modelarse el apego emocional?
La tentación es inmediata: agregar una variable más.
Pero seamos honestos.
El apego emocional:
- no es observable directamente,
- no tiene una escala natural,
- no es comparable entre personas,
- y además tiene incentivos claros para ser exagerado.
Desde el punto de vista matemático, se trata de una variable latente no identificada.
El precio que mi amigo esperaba no estaba explicado solo por los metros cuadrados. Estaba explicado por los años vividos ahí, por los mates compartidos con su novia en el balcón, por las risas con sus hijos en el living. Ninguna columna de mi dataset puede capturar eso, por más que refine la limpieza o agregue features.
La regresión lineal no falla por no capturar el apego emocional.
Falla nuestra expectativa de que todo lo importante sea cuantificable.
Una lectura más honesta del modelo
La regresión lineal puede estimar un precio de mercado frío.
El residuo captura todo lo demás.
Ese residuo no es basura.
Es la parte humana del problema.
Eliminarlo sin pensarlo mejora métricas, pero empobrece la comprensión.
Cierre y continuidad
La regresión lineal es una herramienta matemática simple, pero honesta.
Hace exactamente lo que las matrices dicen que haga.
Cuando un modelo “no cierra”, muchas veces no está fallando el algoritmo.
Está fallando nuestra decisión de qué datos incluir, cuáles excluir y por qué.
Ese departamento “demasiado caro” no rompió mi modelo.
Me obligó a preguntarme qué estaba decidiendo yo al limpiar los datos.
En un caso simple como este, las consecuencias son menores: probablemente ese departamento nunca se venda al precio pretendido. Pero cuando estos mismos criterios se aplican en sistemas más grandes —crédito, seguros, empleo, justicia— las decisiones dejan de ser anecdóticas y pueden llegar a amplificar sesgos, como documenta extensamente Cathy O’Neil en Armas de destrucción matemática.
Porque detrás de cada dato hay una persona.
Y casi siempre, detrás de un outlier, hay una historia.